For
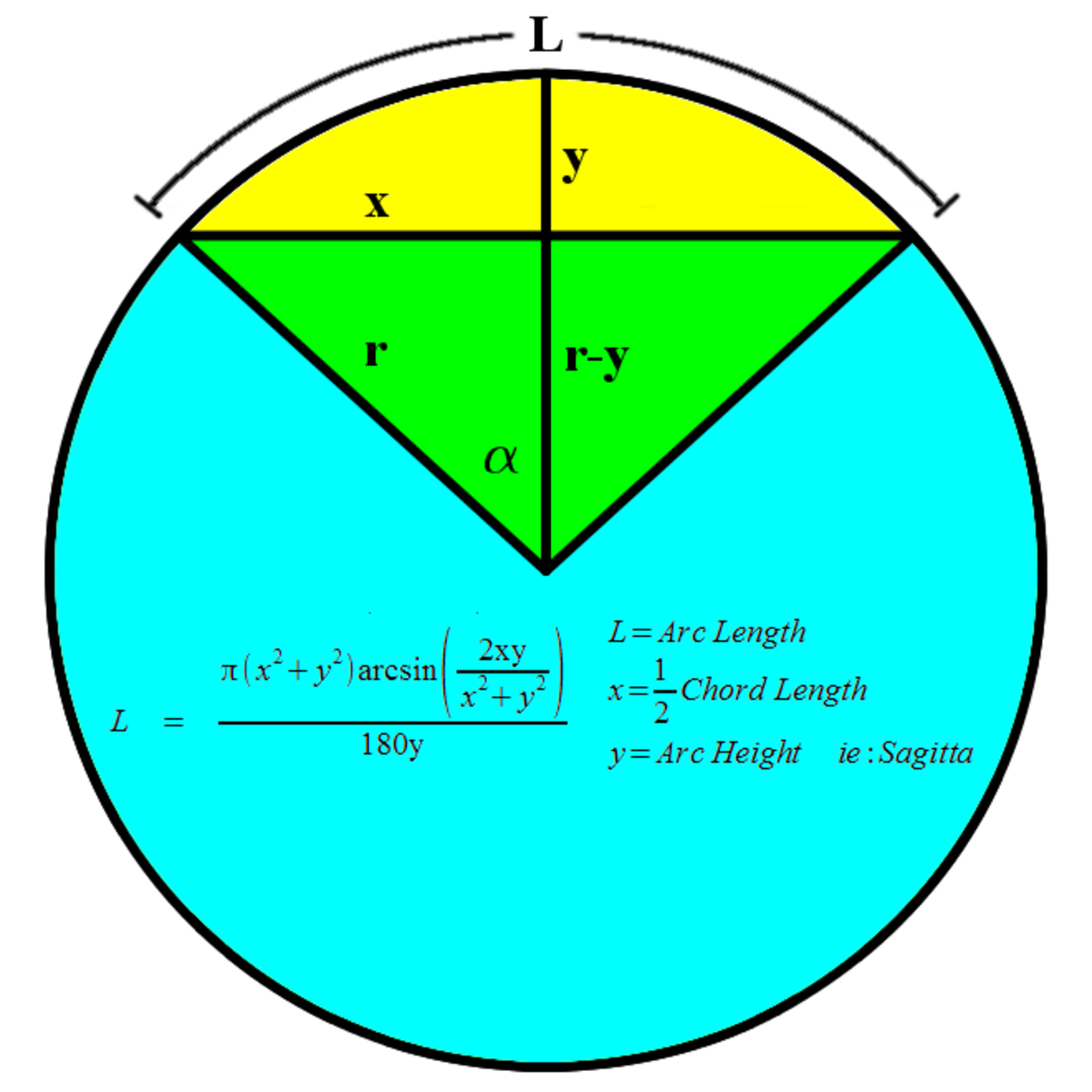
I want a formula that computes distance from chord to circle for any arbitrary point along chord. I have been beating myself up all morning with what little algebra and trig remains trying to figure this out. Sagitta is easy for the center of the chord, but what about at other points?
A little clarity please: distance in the direction of the chord, parallel to sagitta, or in the direction of the radius?
ReplyDeleteSecond, what values might you have: chord length, angle, radius?
If it's the length parallel to sagitta, that distance D = Sagitta - cos * [(1/cos - R], where is the angle of a ray drawn to the top of the distance you are trying to measure. T
Think in small triangles, by extending that ray out, extending your distance needed line up, and draw a line perpendicular to sagitta at the point it exits the circle; knowing that all angles along that ray will be the same as that at the center).
Remember that distance measured is also simply a ratio of X1/X2 = Y1/Y2. Draw a ray from the center of the circle to the top of your distance needed line (where it touches the circle), X1 being the distance from the bottom of the line to be measured to the point the ray crosses the chord, X2 the distance from where the ray crosses the chord to the sagitta, Y1 the distance trying to solve for, Y2 the distance from the chord to the center of the circle (sangitta - Y in your drawing.
I wish I could draw in your comments!
Sorry, I just looked at my notes and noticed I missed an R. It should be
ReplyDeletevertical distance from chord to circle (parallel to sagitta) = sagitta -[cos x [(1/cos) x R - R]]
again, where the is that of the ray from center to the top of your distance being measured.
It's much easier than you are thinking. It all starts with the old SOH CAH TOA pneumonic.
ReplyDeleteI'm going to use a for alpha, to make things easier while typing.
Start with r-y = r*cos(a). This reduces to y = r(1-cos(a)). From this formula, you can calculate the y for any given angle. If you have an angle (b) that measures how far along the arc you have gone, you can find the difference by calculating the y(a) - y(a-b).
Similarly, if you need to calculate based on the distance (d) along the chord, you can calculate that angle from the arctan of (x-d)/(r-y). From there, you should be able to get everything you need.
Do you want the minimum distance from an arbitrary point P on the chord to the circle? Or the length of a segment perpendicular to the chord from point P to the circle?
ReplyDeleteIs this what you are looking for?
ReplyDeleteSagitta - The height of an arc or segment (nice graphic)
https://www.mathopenref.com/sagitta.html
(I dropped out of the University of Florida in 1960 because I never understood what the prof meant!)
JJ
r is radius
ReplyDeleted is distance from center of chord to point P on chord
y is height of chord at its center
z is the chord height at P (height perpendicular to the chord)
alpha = inverse-sin(d/r)
z = r*cos(alpha)-(r-y)
I think ErolB1 got it. Distance from chord to circle at various distances from center of chord.
DeleteThis is definitely the right formula. When I do the calculations on my calculator the numbers are right. When I code it in C, cos(alpha) is wrong. cos returns double, so I cast it to float and the number is wrong.
DeleteUtterly mystified. A for loop calling cos for every value from 0.0f/57.296f to 90.0f/57.296 returns all the right values.
DeleteWild guess, but do your C trig functions all use the same units for angles, or do some use radians and others degrees?
DeleteAll radians. First check that I made.
DeleteMissing minus sign.
ReplyDelete"I want a formula that computes distance from chord to circle for any arbitrary point along chord."
ReplyDeleteTo what point on the circle? Answers would vary, depending on that.